Особенности решения задач с параметрами

Если , то решением неравенства относительно будет , а следовательно, исходное неравенство не может иметь единственного решения. (Неравенство при любом имеет бесконечно много решений.) {LINKS}

Значит, и решением относительно будет . Возвращаясь к , будем иметь . Для того чтобы существовало единственное значение , удовлетворяющее последним неравенствам, необходимо и достаточно, чтобы наименьшее значение квадратного трехчлена равнялось бы 4, т.е. .

Ответ. .

6. Найти все значения , при каждом из которых множество решений неравенства не содержит ни одного решения неравенства .

Решение. Нам надо найти все , такие, что при всех имеет место неравенство . Решение последнего неравенства при данном относительно состоит из двух лучей, исключается внутренняя часть отрезка с концами и (какой из них левый, а какой правый‑неважно). Но если меняется от ‑1 до 1, то меняется от 0 до 1, а меняется от 1 до 3. Теперь понятно, что не может принимать значения от 0 до 3, а при всех или заданное условие выполняется.

Ответ. .

Графические методы решения задач с параметрами.

Задачи с параметрами требуют к себе своеобразного подхода по сравнению с остальными – здесь необходимо грамотное и тщательное исследование. Для применения графических методов требуется умение выполнять построение различных графиков, вести графическое исследование, соответствующее данным значениям параметра.

1. При каких значениях параметра уравнение имеет ровно 2 решения?

Решение. Рассмотрим функцию .

Графиком такой функции является ломанная из трех звеньев. Найдем точки излома:

1) ;

2) .

Так как ; 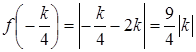, то и 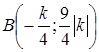‑ точки излома. Заметим, что , если и имеет минимум в одной из точек или .

С геометрической точки зрения количество решений уравнения ‑ это количество точек пересечения при каждом фиксированном значении параметра ‑ ломанной, состоящей из трех звеньев, и прямой .

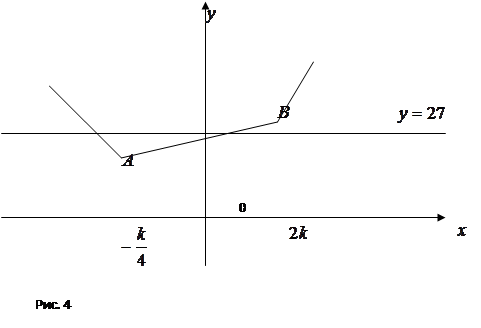
По рис. 4 видно, что уравнение имеет ровно 2 решения, если значение в точке минимума меньше 27. Причем значение в другой из точек излома несущественно. Значит необходимо выполнение одного из двух неравенств:

Великая педагогика:

Технология коллективной мыследеятельности
Д. Г. Левитес в 1990 году познакомился с технологией коллективной мыследеятельности (КМД) в Нижнем Новгороде на семинаре. Автор этой дидактической системы — профессор К. Я. Вазина, заведующая кафедрой «Деятельность» Нижегородского межобластного института повышения квалификации работников профтехобр ...

Теоретические основы индивидуального подхода к одаренным детям
Выражение « Одаренный ребенок» употребляется весьма широко. Если ребенок обнаруживает необычные успехи в учебных или творческих занятиях, значительно превосходит сверстников, его могут назвать одаренным. Если у ребенка необыкновенно быстрый темп умственного развития, вполне правомерно назвать его н ...

Обобщение опыта работы преподавателей по развитию орфографической зоркости у младшего школьника
Как научить правильно писать – эта проблема всегда волновала учителей и ученых. Как сделать так, чтобы количество ошибок уменьшалось, а письмо стало бы более осознанным и правильным. Хорошо, когда ребенку «дано» от Бога: правила чувствует интуитивно и пишет правильно. Но ведь таких единицы. Известн ...