Особенности решения задач с параметрами

Ответ. .

3. При каких значениях параметра квадратное уравнение имеет корни одного знака? {LINKS}

Решение. Так как по условию задачи рассматриваемое уравнение – квадратное, то (иначе формулировка задачи не имеет смысла). Очевидно, условие задачи предполагает также существование корней квадратного уравнения, что означает неотрицательность дискриминанта. Если , то квадратное уравнение имеет один корень (два равных корня).

Так как по условию корни должны быть одинаковых знаков, то

, т.е. .

Решением последнего неравенства является

.

С учетом услови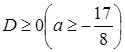й и получим .

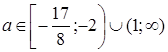Ответ. 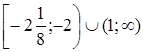[7].

4. Для каждого неотрицательного значения параметра решить неравенство .

Решение. Левая часть неравенства представляет собой многочлен как относительно , так и относительно параметра . Степени соответственно равны 4 и 3. Однако если умножить многочлен на , а затем сделать замену , то в новом многочлене максимальная степень параметра будет равна 2. Случай дает нам ответ . Будем теперь считать, что . Умножив обе части неравенства на и сделав замену , получим

.

Левая часть представляет собой квадратный трехчлен относительно :

,

.

Раскрывая левую часть неравенства на множители, получим

,

или

.

Второй множитель положителен при всех , если . Приходим к неравенству , откуда, если , ; если , ‑ любое. Возвращаясь к , получим ответ.

Ответ. Если , то ;

если , то ;

если , то ‑ любое [21].

5. Найти все значения параметра , при которых существует единственное значение , при котором выполняется неравенство

.

Решение. Обозначим () и перейдем к основанию 5. Получим:

.

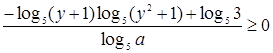Функция от , расположенная в числителе, монотонно убывает. Нетрудно подобрать значение , при котором она обращается в нуль:.

Великая педагогика:

Физическое воспитание и развитие навыков ходьбы
Одной из важнейших задач физического воспитания незрячих и частичновидящих детей является коррекция двигательных недостатков, возникших в результате дефекта. Нарушения и аномалии зрительной системы отрицательно сказываются на формировании двигательных способностей – силы, быстроты, выносливости, ко ...

Психолого-педагогические основы установления контактов с семьей школьника
Прежде чем перейти к характеристике основных форм и методов работы учителей с родителями учащихся, необходимо остановиться на выявлении некоторых психолого-педагогических правил их взаимодействия и способах установления контактов с семьей. Первое правило:В основе работы школы и классного руководите ...

Психолого – педагогическая характеристика интереса
Одной из педагогических наук, которая изучает закономерности музыкального воспитания с целью совершенствования его содержания и методов, является методика музыкального воспитания. Она практикует, как на основе дидактических принципов и методов целесообразно строить учебно – воспитательный процесс и ...