Особенности решения задач с параметрами
![]() или
или 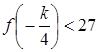 .
.
Так как ![]() , то первое неравенство равносильно неравенству
, то первое неравенство равносильно неравенству ![]() . А поскольку
. А поскольку 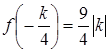 , то второе неравенство равносильно неравенству
{LINKS}
, то второе неравенство равносильно неравенству
{LINKS}
![]() .
.
Объединением полученных интервалов будет интервал ![]() .
.
Ответ. Уравнение имеет два решения при ![]() [7].
[7].
2. При любом значении параметра ![]() решить неравенство
решить неравенство
![]() .
.
Решение. Рассмотрим плоскость ![]() и изобразим на ней множество точек, координаты которых удовлетворяют неравенству рис.5. Сначала изобразим область, для точек которой имеет смысл
и изобразим на ней множество точек, координаты которых удовлетворяют неравенству рис.5. Сначала изобразим область, для точек которой имеет смысл ![]() . Это будет полуплоскость
. Это будет полуплоскость ![]() (правее и ниже прямой
(правее и ниже прямой ![]() ), из которой удалены части прямых
), из которой удалены части прямых ![]() . Вне полосы, ограниченной прямыми
. Вне полосы, ограниченной прямыми ![]() и
и ![]() , будет
, будет ![]() , и, следовательно, после потенцирования неравенства получим
, и, следовательно, после потенцирования неравенства получим ![]() .
.
Последнему неравенству соответствует область под параболой ![]() (при этом
(при этом ![]() ).
).
Внутри полосы ![]() будет
будет ![]() . На рисунке 5 область
. На рисунке 5 область ![]() , для точек которой
, для точек которой ![]() , заштрихована. (Заметим, что парабола
, заштрихована. (Заметим, что парабола ![]() касается прямой
касается прямой ![]() ) Теперь ось
) Теперь ось ![]() точками
точками ![]() разбита на шесть участков, на каждом из которых легко выписывается решение нашего неравенства. Для этого берем
разбита на шесть участков, на каждом из которых легко выписывается решение нашего неравенства. Для этого берем ![]() на соответствующем участке, проводим горизонтальную прямую, находим значения
на соответствующем участке, проводим горизонтальную прямую, находим значения ![]() , соответствующие концам отрезков этой прямой, попавших в заштрихованную зону.
, соответствующие концам отрезков этой прямой, попавших в заштрихованную зону.

Например, если ![]() , то получаем два отрезка, концы первого:
, то получаем два отрезка, концы первого: ![]() и
и 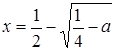 (меньший корень уравнения
(меньший корень уравнения ![]() ), второго:
), второго:![]() и
и 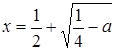 .
.
Ответ. Если ![]() ,
, ![]() , решений нет;
, решений нет;
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то 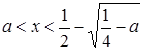 и
и 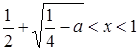 ;
;
если ![]() , то
, то 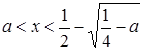 и
и 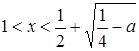 ;
;
если ![]() , то
, то 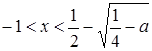 и
и 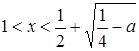 ;
;
если ![]() , то
, то ![]() ;
;
если ![]() , то
, то 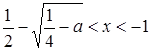 и
и 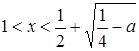 [4].
[4].
Великая педагогика:
Особенности детей из социально-неблагополучных семей
Характеристика неблагополучных семей очень разнообразна – это могут быть семьи, где родители жестоко обращаются с детьми, не занимаются их воспитанием, где родители ведут аморальный образ жизни, занимаются эксплуатацией детей, бросают детей, запугивают их «для их же блага», не создают условий для н ...
Педагогические рекомендации для работников ДОУ по использованию
художественной литературы для развития количественных представлений 5-го года
жизни
Иногда дошкольники, хорошо понимая условность художественного произведения, как бы «отстраняются» от него, от его персонажей, от их бед и страданий. Такой уход, с одной стороны, способствует сохранению жизнерадостного, безмятежного, ничем не омраченного эмоционального состояния; с другой - дети, не ...
Педагогика высшей школы
Педагогика высшей школы – педагогика институтов, академий, университетов. Данная отрасль относится и к возрастной и к отраслевой педагогике, т.к. высшая школа – образовательное учреждение наивысшего ранга, занимающееся подготовкой высококвалифицированных профессионалов и являющееся конечной ступень ...
Категории
- Главная
- Планирование образовательного процесса
- Индивидуальное развитие детей-сирот
- Современные технологии обучения
- Инновация и новизна в педагогике
- Самоопределение старшеклассников
- Активные методы обучения
- Педагогическая информация
