Методика решения уравнений и неравенств

Ответ. [17].

Тригонометрические неравенства.

Тригонометрическими неравенствами называются неравенства вида , где ‑ одна из тригонометрических функций . При решении этих неравенств удобно использовать график соответствующей тригонометрической функции. {LINKS}

1. Решить неравенство:.

Решение. Здесь должно выполняться условие , т.е. . Произведем преобразования:

.

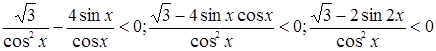Так как при , то достаточно решить неравенство , т.е. . Полагая и построив график функции (рис. 2), устанавливаем, что

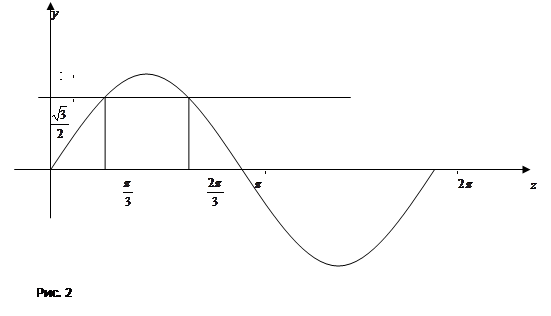
или . В эти интервалы значения не входят.

Ответ. 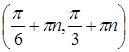, где .

2. Решить неравенство:.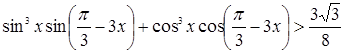

Решение. Преобразуем левую часть равенства:

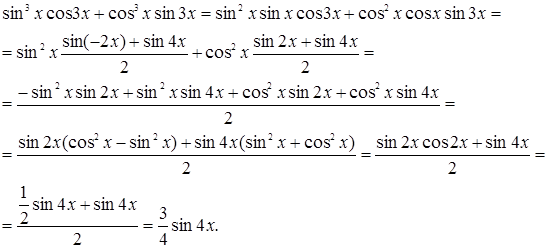
Остается решить неравенство 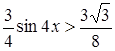, т.е. . Полагая и построив график функции (рис.2) находим

или . Отсюда .

Ответ. .

3. Решить неравенство:.

Решение. Последовательно преобразуя левую часть неравенства, получим

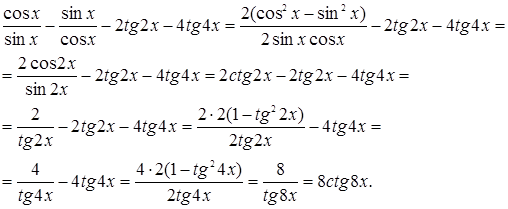
Итак, имеем неравенство или . Полагая , с помощью графика функции (рис.3),

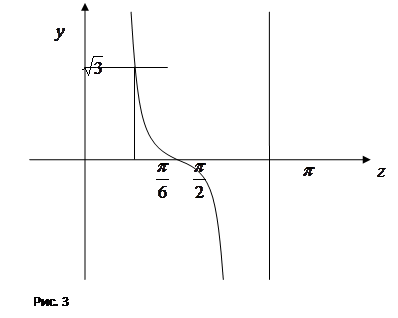
устанавливаем, что

, откуда , т.е. , .

Великая педагогика:

Анализ программного материала и ГОСО. РК по музыкальному воспитанию детей дошкольного возраста
Современные программы, используемые в Республике Казахстан "Кайнар", "Балбобек", а также российские программы "Радуга", "Детство", "Развитие", "Школа 2100" нацеливают педагогов на формирование широкой двигательной культуры дошкольников. Ан ...

Сущность психолого-педагогического сопровождения учащихся в школе в поддержке здорового образа жизни
Сопровождение – это совместное передвижение, прохождение с кем-либо части его пути в качестве спутника или провожатого, помощь одного человека другому в преодолении трудностей и помощь, запускающая механизм собственных ресурсов человека. А сопровождающий – это человек, который лишь временно находит ...

Психология незрячих
Развитие психики при нарушениях зрения Одной из наиболее актуальных проблем специальной психологии является проблема межличностного взаимодействия инвалидов и физически здоровых людей. Изучение психики людей с ограниченными физическими возможностями, осознание трудностей, связанных с вхождением дет ...