Методика решения уравнений и неравенств

Докажем единственность отрицательного корня. Можно поступить следующим образом. Рассмотрим функции

.

Докажем, что если , то . (Из этого будет следовать наше утверждение, поскольку в данном случае возрастает везде, где .) {LINKS}

Имеем

.

Значит, 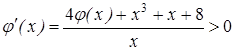при .

Утверждение доказано.

2. Найти все целые значения x, удовлетворяющие неравенству

.

Решение. Область определения левой части неравенства . Значит, нам достаточно рассмотреть три значения x: 1, 2, 3.

Если , то левая часть равна .

Если , то .

Если , то .

Ответ. 1; 2.

3. Найти все целые x, удовлетворяющие неравенству

.

Решение. Рассмотрим функцию .

Докажем, что, начиная с некоторого x, f (x) возрастает. Это можно было сделать обычным путем, оценивая производную. Мы сделаем иначе. Нам достаточно доказать возрастание функции для целых x, т.е. что

.

Имеем

.

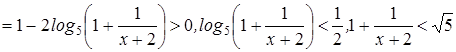Последнее неравенство выполняется при , т.е. для всех допустимых целых x.

Нам осталось найти наибольшее целое, для которого (или наименьшее, для которого ).

Докажем, что

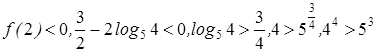. Далее,.

Ответ. -1, 0, 1, 2 [22].

Тригонометрические уравнения.

К нестандартным следует отнести также уравнения, содержащие обратные тригонометрические функции.

1. Решить уравнение:.

Решение. По определению обратных тригонометрических функций

. Найдем .

Эта задача сводится к следующей: «Найти cos α, если и

()».

Великая педагогика:

Самостоятельная работа как высшая форма учебной деятельности
Обычно, говоря об учебной деятельности, исследователи имеют в виду работу ученика в классе. Но организация учебной деятельности школьника включает наряду с классной его домашнюю, внеклассную и самостоятельную работу по предмету. Наименее изученной и, в то же время, представляющей наибольший интерес ...

Восприятие времени
В отличие от ощущений в образе восприятия субъекту дано не только представление о времени как таковом, но и представление о его размерности. В восприятии время дифференцируется, дробится на отрезки, ин­тервалы. Появляется переживание не просто длительности или последователь­ности, но и определенной ...

Особенности педагогического контроля усвоения содержания образования и оценка результатов образовательного процесса
Контроль знаний учащихся как основной элемент оценки качества образования Особенности педагогического контроля и оценки успеваемости учащихся Контроль знаний учащихся как основной элемент оценки качества образования Контроль знаний учащихся является одним из основных элементов оценки качества образ ...