Методика решения уравнений и неравенств

Основные идеи этого пункта достаточно хорошо видны из примеров:

1. Решить уравнение:.

Решение. Левая часть данного уравнения не превосходит 2, а правая- не меньше 2. Следовательно, равенство может иметь место лишь при условии, что левая и правая части равны 2, т.е. x = 0. {LINKS}

Замечание. Данная ситуация, когда наименьшее значение функции, расположенной в одной части уравнения, равно наибольшему значению функции, расположенной в другой части, может быть обобщена. Более общий случай – уравнения вида f (x) = φ (x), для которых при всех допустимых x (формально мы можем переписать это уравнение в виде

f (x) = φ (x) = 0, в результате приходим к уже рассмотренной ситуации, поскольку наибольшее значение правой части равно нулю).

2. Решить уравнение:.

Докажем, что данное уравнение не имеет решений. Перейдем к следствию (потенцируем): .

Оценим левую часть на основании неравенства между средним геометрическим и средним арифметическим

:

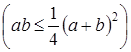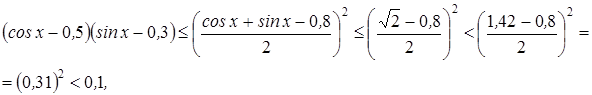
т.е. левая часть меньше правой. Уравнение не имеет решений.

Ответ. Нет решения.

3. Решить систему уравнений: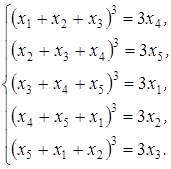

Решение. Докажем, что .

Пусть для определенности x5 > x4, тогда из первых двух уравнений получим , откуда и тем более . Далее из третьего и четвертого получаем и тем более . Из последней пары находим . Получилось противоречие ( и , т.е. , а предположили, что ).

Значит, , отсюда и т.д., все неизвестные равны между собой.

Ответ. (0, 0, 0, 0,0); .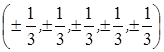

Нестандартные по формулировке задачи, связанные с уравнениями или неравенствами.

К данной категории, в частности, относятся задачи, в которых требуется определить число корней заданного уравнения, доказать существование корня на определенном промежутке, решить уравнение или неравенство на заданном промежутке. Рассмотрим несколько примеров.

1. Доказать, что уравнение имеет одно положительное решение и одно отрицательное решение.

Решение. Единственность положительного решения достаточно очевидна. Это следует из того, что при , где f (x)-левая часть заданного уравнения, т.е. f(x) при монотонно возрастает, а .

Великая педагогика:

Формы организации обучения с использованием активных методов в ВУЗе
Существуют имитационные и неимитационные формы организации обучения с использованием активных методов обучения. Рассмотрим характеристику неимитационных методов: лекции, семинары, дискуссии, коллективную мыслительную деятельность. Лекции - нетрадиционная форма проведения Проблемная лекция начинаетс ...

Значение урока русского языка. Понятие словарного запаса
В системе начального образования предмет «Русский язык» занимает центральное место. Как средство познания действительности русский язык обеспечивает интеллектуальное развитие ребёнка, формирует его понятийно- категориальный аппарат, развивает абстрактное мышление, память и воображение. Он позволяет ...

Психологические особенности младших школьников
«Человек, испытавший радость творчества даже в самой минимальной степени, углубляет свой жизненный опыт и становится иным по психическому складу», - утверждал Б.В. Асафьев. «Ранее вовлечение детей (и не только особо одаренных) в творческую деятельность очень полезно для общего художественного разви ...