Методика решения уравнений и неравенств

Поскольку cos α>0, то .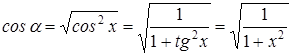

Получаем уравнение 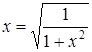, откуда . Получаем для x два значения: {LINKS}

.

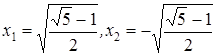Второе значение для x не подходит, поскольку .

Ответ. .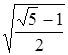

Замечание. Данное уравнение можно решить и иначе. Обозначим левую и правую части данного уравнения через y . Тогда . Для y имеем тригонометрическое уравнение, сводящееся к квадратному относительно

По смыслу задачи , следовательно, , значит,

.

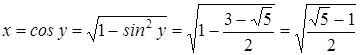Не так уж редко встречаются уравнения, решение которых основывается на ограниченности функций cos x и sin x .

2. Решить уравнение:.

Решение. Поскольку , то левая часть не

превосходит 3 и равна 3, если .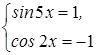

Для нахождения значений x, удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них. Затем среди найденных значений отберем те, которые удовлетворяют и другому.

Начнем со второго: .

Тогда .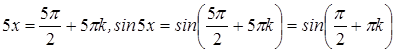

Понятно, что лишь для четных k будет .

Ответ. [2].

Найти в градусах корень уравнения:, если .

Решение. Уравнение является однородным второго порядка. Разделив обе части на , получим уравнение , квадратное относительно . Решив его, найдем

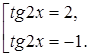
По условию , значит, . При этих значениях аргумента , следовательно, уравнение не имеет решения.

Из уравнения находим . Значит, . Придавая значения , выбираем , удовлетворяющие условию . При получим .

Великая педагогика:

Методы и приемы изучения состава слов
Знакомство со значащими частями слова, с морфемным составом слова программа предполагает во втором классе. Дается слово лес, к нему подбираются слова: лесок, лесник, лесной. Вводится термин «корень» и «однокоренные слова»; в понятие «корень» будет входить признак: главная смысловая часть, общая для ...

Описание кабинета биологии
Кабинет биологии состоит из 2 смежных комнат: класс-лаборатория площадью 45,34 м2 и лаборантская комната площадью 17,2 м2. Кабинет расположен на третьем этаже с ориентировкой окон на юг. Кабинет биологии обеспечен столами (15 штук) с пластиковым покрытием. Электрическая сеть не подведена к ученичес ...

Мотивация изучения математических понятий
Начальным этапом формирования понятий является мотивация. Сущность этого этапа заключается в подчеркивании важности изучения понятия, в побуждении школьников к целенаправленной и активной деятельности, в возбуждении интереса к изучению понятия. Мотивация может осуществляться как по средствам привле ...