Мотивация изучения теорем

Мотив изучения и необходимость доказательства теоремы показаны.

Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.

Например, перед доказательством теоремы «В равнобедренном треугольнике углы при основании равны» учащимся предлагается решить задачу: {LINKS}

В равнобедренном треугольнике АВС (АВ=ВС) вершина угла В соединена с серединой К стороны АС отрезком. Докажите, что треугольники АВК и СВК равны. Достаточно ли этих данных, чтобы установить равенство названных треугольников.

Так как третьего признака равенства по трем сторона у учащихся пока нет, то данную задачу они решить не могут. Созданная проблемная ситуация позволяет сразу мотивировать необходимость изучения сразу трех теорем : «В равнобедренном треугольнике углы при основании равны», «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой», «Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны».

Прием 4. Показ, как решалась данная проблема в истории науки.

Например, перед изучением второго признака равенства треугольников, можно привести историческую справку.

В

В древние времена, для определения расстояния от берега до морских кораблей, Фалес Милетский (философ древней Греции) использовал следующий способ:

Рис 2

Е

С Д А

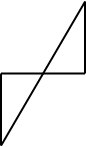Пусть А – точка берега (рис.2), В – корабль на море. Для определения расстояния АВ восстанавливают на берегу перпендикуляр произвольной длины: АС⊥АВ; в противоположном направлении восстанавливают СЕ⊥АС так, чтобы точка Д (середина АС), В и Е находились на одной прямой. Тогда СЕ будет равна искомому расстоянию АВ.[4]

После этой справки учитель задает вопрос, а прав ли Фалес, утверждая, что СЕ=АВ. Ответы учеников могут разделиться. Далее учитель вводит теорему: «Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны». Пользуясь данной теоремой, ученики без труда ответят, что треугольники АВД и СЕД равны, а значит и соответственные стороны АВ и СЕ равны.

Проследим мотивационный этап работы над теоремой на примере теоремы: «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой».

Один из приемов мотивации изучения данной теоремы – знание теоремы для решения задач.

В

С

Можно использовать другой прием, показав конструкцию строительной фермы (рис.3), где АС=СВ, АД=ДВ, ДМ=МВ; простейшую конструкцию стропил (рис.4) АВ=ВС и АК=КС, то есть наблюдение жизненных фактов.

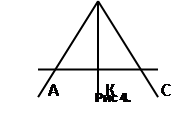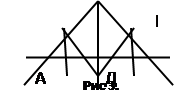Великая педагогика:

Народная сказка как средство обогащения экспрессивной лексики старших дошкольников
Народная сказка, являясь доступной пониманию ребенка старшего дошкольного возраста, является могучим средством формирования образности речи. Именно в русской народной сказке имеется наличие всех необходимых элементов образности, сказка оказывает большое воспитательное и обучающее влияние на ребенка ...

Восприятие и представление
В обыденной жизни слово «представление» употребляется в различных значениях. Оно может означать понимание, выра­жаемое, например, вопросом: «Ты представляешь себе, что ты натворил?», упо­требляться в значении знания о чем-то, например в высказывании «Я не пред­ставляю себе [не знаю], что это такое» ...

Усвоение детьми различных групп слов
В рамках нашей темы существует еще одна проблема, которая связана с трудностями усвоения учащимися отдельных групп слов. Наблюдения за работой учителей начальных классов показывают, что на уроках русского языка, классного и внеклассного чтения уделяется недостаточное внимание работе с отвлеченными ...