Правила и теоремы теории вероятностей

Формула Бейеса

Пусть в условиях рассуждения, относящегося к формуле полной вероятности, произведено одно испытание, в результате которого произошло событие А. Спрашивается: как изменились (в связи с тем, что событие А уже произошло) ве­личины P(Bk), k = 1, . , п. {LINKS}

Найдем условную вероятность РA(Вk).

По теореме умножения вероятностей и формуле (3) имеем:

Отсюда:

Наконец, используя формулу полной вероятности, находим

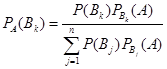(k=1, 2, …, n). (7)

Формулу(7) называют формулой Бейеса (Байеса)

Пример. Большая популяция людей разбита на две группы одинаковой численности. Диета одной группы отличалась высоким содержанием ненасыщенных жиров, а диета контрольной группы была богата насыщенными жирами. После 10 лет пребывания на этих диетах возникновение сердечнососудистых заболеваний составило в этих группах соответственно 31% и 48%. Случайно выбранный из популяции человек имеет сердечно-сосудистое заболевание. Какова вероятность того, что этот человек принадлежит к контрольной группе?

Введем обозначения для событий:

А - случайно выбранный из популяции человек имеет сердечно-сосудистое заболевание;

B1 - человек придерживался специальной диеты;

В2 - человек принадлежал к контрольной группе. Имеем

Р(В1) = Р(В2) = 0,5,

(A) = 0,31, (A) = 0,48.

Согласно формуле полной вероятности

Р(А) = 0,5 ∙ 0,31 + 0,5 ∙ 0,48 = 0,395

и, наконец, в силу формулы (7) искомая вероятность

.

Таким образом, можно привести много разнообразных примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей. Она занимается математическим анализом случайных событий и связанных с ними случайных величин.

Для решения задач по теории вероятностей следует применять следующие теоремы: сложения вероятностей несовместимых событий, умножения вероятностей, сложений вероятностей совместимых событий; формулы: полной вероятности, Бейеса (Байеса).

Одной из форм дифференцированного обучения по курсу теории вероятностей может являться факультативный курс.

Великая педагогика:

Сравнительный анализ ФЕЗ с их эквивалентами в русском языке
Объектом исследования послужили фразеологические единицы с компонентом-зооморфизмом, отобранные из Англо-русского фразеологического словаря А.В.Кунина [1967]. Среди них встречаются наиболее частотные зоонимы cat (123), dog (289), horse (80), bear (60), bird (45), goose (50). При рассмотрении особен ...

Организация содержания игр и упражнений для развития сенсорной сферы детей младшего дошкольного возраста
Сенсорное воспитание – это развитие восприятия ребенком и формирование представлений о внешних свойствах и качествах предметов: форме, цвете, величине, положении в пространстве, запахе, вкусе и так далее. С восприятия предметов и явлений окружающего мира начинается познание ребенка. Поэтому нормаль ...

Значение использования художественной литературы в умственном развитии детей
Что же дает ребенку художественная литература, в части сказка? Как влияет на формирование его личности? Сказка активизирует воображение ребенка, заставляет его сопереживать, внутренне содействовать персонажам, а в результате этого сопереживания у ребенка появляются не только новые знания и представ ...