Особенности решения текстовых задач

Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи.

В каждой задаче можно выделить:

а) числовые значения величин, которые называются данными, или известными (их должно быть не меньше двух); {LINKS}

б) некоторую систему функциональных зависимостей в неявной форме, взаимно связывающих искомое с данными и данные между собой (словесный материал, указывающий на характер связей между данными и искомыми);

в) требование или вопрос, на который надо найти ответ.

Числовые значения величин и существующие между ними зависимости, т.е. количественные и качественные характеристики объектов задачи и отношений между ними, называют условием (или условиями) задачи. В задаче обычно не одно, а несколько условий, которые называют элементарными.

Требования могут быть сформулированы как в вопросительной, так и в повествовательной форме, их также может быть несколько. Величину, значения которой требуется найти, называют искомой величиной, а числовые значения искомых величин – искомыми, или неизвестными.

Систему взаимосвязанных условий и требований называют высказывательной моделью задачи. Для того чтобы уяснить структуру задачи, надо выявить ее условия и требования, т.е. построить высказывательную модель задачи.

1. Из пункта А одновременно стартуют три бегуна и одновременно финишируют в том же пункте, пробежав по маршруту, состоящему из прямолинейных отрезков АВ, ВС, СА, образующих треугольник АВС. На каждом из указанных отрезков скорости у бегунов постоянны и равны: у первого – 10 км / ч, 16 км / ч и 14 км / ч соответственно; у второго – 12 км / ч, 10 км / ч и 16 км / ч соответственно. Третий бегун в пунктах В и С оказывается не один и меняет скорость на маршруте один раз. Установить, является ли треугольник АВС остроугольным или тупоугольным.

Решение . Обозначим стороны треугольника: . Из условия следует, что первый и последний участки - и - третий бегун пробегает вместе с первым либо со вторым; причем, если маршрут он бежит вместе с первым, то маршрут - вместе с первым, и наоборот. А поскольку он меняет скорость один раз, то его скорости на участках , и соответственно могут быть равными:

1) 10, 10, 16; 3) 12, 12, 14;

2) 10, 16, 16; 4) 12, 14, 14;

Первый вариант отпадает сразу, так как в этом случае третий бегун отстанет от второго.

По аналогичной причине отпадает второй вариант (третий бегун обгонит первого). Остаются два варианта. Соответственно имеем две системы (уравнения составляются на основании условия равенства времени, затрачиваемого на маршрут бегунам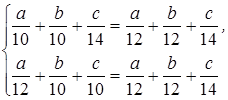и):

и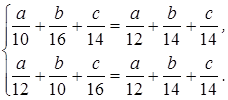

Для каждой системы легко выразить и через . Для первой системы , , - наибольшая сторона; причем < и >, так как 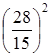>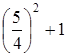. Треугольник тупоугольный. Для второй системы >т.е. этот случай невозможен.

Великая педагогика:

Методика развития психофизических качеств
Быстрота как психофизическое качество — это способность выполнять двигательные действия в минимальный срок, которая определяется скоростью реакции на сигнал и частотой многократно повторяющихся действий. Предполагается, что выполнение двигательной задачи кратковременно и не вызывает у ребенка утомл ...

Психолого-педагогические особенности развития речи детей младшего дошкольного возраста
По мнению Д.Б. Эльконина дошкольный возраст 3-4 лет является периодом интенсивного психического развития. Особенности этого этапа проявляются в прогрессивных изменениях во всех сферах, начиная от совершенствования психофизиологических функций и кончая возникновением сложных личностных новообразован ...

Проблемы формирования и развития грамматических навыков и пути их решения
Грамматика является структурой языка. Грамматика превращает язык в речь. Изучение грамматики неизбежно при овладении иностранным языком. Как считает автор методической статьи , из трех аспектов языка - фонетики, лексики и грамматики, именно при овладении грамматикой английского языка школьники, и п ...