Производная и ее применение

Равенство (при нечетном п) позволяет выразить корень нечетной степени из отрицательного числа через арифметический корень той же степени. Например,. {LINKS}

Замечание. Для любого действительного х

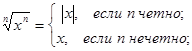
Замечание. Удобно считать, что корень первой степени из числа а равен а. Как вы уже знаете, корень второй степени из числа называют квадратным корнем, а показатель 2 корня при записи опускают (например, корень квадратный из 7 обозначают просто ) Корень третьей степени называют кубическим корнем.

2. Основные свойства корней. Напомним известные вам свойства арифметических корней л-й степени.

Для любого натурального п, целого k и любых неотрицательных чисел а и b выполнены равенства:

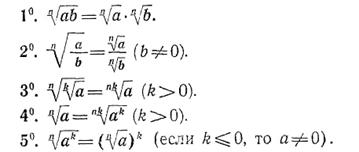
Докажем свойство 10. По определению — это такое неотрицательное число, п-я степень которого равна ab. Число · неотрицательно. Поэтому достаточно проверить справедливость равенства (·)п=ab которое вытекает из свойств степени с натуральным показателем и определения корня n-й степени: (·)п=()n()n=ab

Аналогично доказываются следующие три свойства:

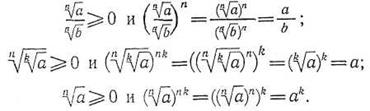
Докажем теперь свойство 50. Заметим, что n-я степень числа ()k равна ak:

По определению арифметического корня ()k=k (так как ).

Великая педагогика:

Принципы профессионального обучения и особенности их реализации при подготовке бакалавров во Франции
Главным принципом обучения в целом (не только профессионального) является доступность образования. Существует, как позитивная, так и негативная оценка этого принципа. Критикуют реализацию этого принципа по причине укоренившегося стереотипа о том, что образование дает человеку не столько возможность ...

Технология социально-педагогической поддержки старшеклассников в профессиональном самоопределении
Учитывая нарастающие темпы преобразований в обществе, и, следуя очевидной логике Концепции модернизации российского образования, которая предполагает ориентацию образовательной системы на новое качество, возможно, предположить, что педагогическая поддержка старшеклассников в профессиональном самооп ...

Специфика индивидуального подхода в психологии и педагогике
Прогрессивные педагоги во все времена уделяли повышенное внимание вопросу об индивидуальном подходе к детям. В высказываниях по этому поводу подчеркивается значение индивидуального подхода для всестороннего развития личности ребенка, ориентировка педагога на гуманное отношение к ребенку, уважение е ...