Мотивация изучения математических понятий

Начальным этапом формирования понятий является мотивация. Сущность этого этапа заключается в подчеркивании важности изучения понятия, в побуждении школьников к целенаправленной и активной деятельности, в возбуждении интереса к изучению понятия. Мотивация может осуществляться как по средствам привлечения средств нематематического содержания (внешняя мотивация), так и в ходе выполнения специальных упражнений, объясняющих необходимость развития математических теорий (внутренняя мотивация). Например, появление обыкновенных дробей, как правило, мотивируется потребностями практики. Введение смежных углов можно мотивировать необходимостью изучения не только отдельных фигур, но и их объединений. Рассмотрение взаимного расположения прямой и окружности приводит к трем случаям, один из которых характерен тем, что окружность и прямая имеют одну общую точку. Указанный случай и обуславливает введение понятия касательной к окружности. {LINKS}

Примеры:

1. Арифметическая (геометрическая) прогрессия может быть введена путем выполнения упражнений на запись числовых последовательностей, заданных определенными свойствами, либо на выявление свойств, которыми обладают указанные последовательности.

Например, при введении понятия арифметическая прогрессия можно предложить следующее задание:

Дана последовательность чисел: 4, 7, 10, 13, 16, ….

Ответьте на следующие вопросы:

Какая закономерность прослеживается между числами? (последующее число отличается от предыдущего на 3);

Попробуйте выразить 3-ий член, 4-ый член, n-ый член через первый;

Таким образом, обозначив первый член последовательности через а1, второй – а2, и так далее, а n-ый через аn, мы можем сделать соответствующие выводы: аn=an-1 + 3; разность между элементами равна 3, обозначим это число через d, тогда аn=an-1 + d, аn=a1 + (n – 1)d. Рассмотренная числовая последовательность называется арифметической.

Определение: числовую последовательность, каждый член которой, начиная со второго, равен сумме предшествующего члена и одного и того же числа d, называют арифметической прогрессией, а число d – разностью арифметической прогрессии.

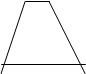
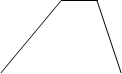
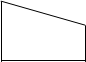
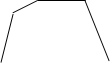
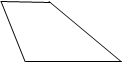
2. Ознакомление с существенными свойствами трапеции может осуществляться посредством предъявления учителем рисунка, на котором изображены различные четырехугольники, и выделения учащимися тех из них, у которых две стороны параллельны, а две другие нет.

а б в г

д е ж з

и

Рассматривая эти рисунки, учащиеся должны ответить на вопрос: «Какие из данных фигур имеют общие свойства?» Ребята замечают, что в четырехугольниках а, б, г, д, и две противоположные стороны параллельны, а две другие нет. После этого им сообщается, что такой четырехугольник называется трапецией.

Великая педагогика:

Технология социально-педагогической поддержки старшеклассников в профессиональном самоопределении
Учитывая нарастающие темпы преобразований в обществе, и, следуя очевидной логике Концепции модернизации российского образования, которая предполагает ориентацию образовательной системы на новое качество, возможно, предположить, что педагогическая поддержка старшеклассников в профессиональном самооп ...

Компьютерные технологии обучения на уроках физической культуры в старших классах
Компьютерные технологии позволяют модифицировать учебный процесс и гарантируют большую эффективность в достижении результатов обучения. Использование компьютерных технологий существенно обогащает педагогические методы обучения школьников. Возможности компьютерных технологий (электронных учебных пос ...

Сущностная характеристика феномена одаренности
Одаренность может рассматриваться с нескольких точек зрения. Одни рассматривают ее как совокупность способностей, внутренних задатков и предпосылок. Таким образом, одаренность от слова « дар». Приведем несколько таких определений: Одаренность – особо благоприятные внутренние предпосылки развития. Л ...