Мотивация изучения теорем

Мотив изучения и необходимость доказательства теоремы показаны.

Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.

Например, перед доказательством теоремы «В равнобедренном треугольнике углы при основании равны» учащимся предлагается решить задачу: {LINKS}

В равнобедренном треугольнике АВС (АВ=ВС) вершина угла В соединена с серединой К стороны АС отрезком. Докажите, что треугольники АВК и СВК равны. Достаточно ли этих данных, чтобы установить равенство названных треугольников.

Так как третьего признака равенства по трем сторона у учащихся пока нет, то данную задачу они решить не могут. Созданная проблемная ситуация позволяет сразу мотивировать необходимость изучения сразу трех теорем : «В равнобедренном треугольнике углы при основании равны», «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой», «Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны».

Прием 4. Показ, как решалась данная проблема в истории науки.

Например, перед изучением второго признака равенства треугольников, можно привести историческую справку.

В

В древние времена, для определения расстояния от берега до морских кораблей, Фалес Милетский (философ древней Греции) использовал следующий способ:

Рис 2

Е

С Д А

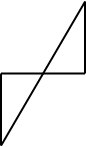Пусть А – точка берега (рис.2), В – корабль на море. Для определения расстояния АВ восстанавливают на берегу перпендикуляр произвольной длины: АС⊥АВ; в противоположном направлении восстанавливают СЕ⊥АС так, чтобы точка Д (середина АС), В и Е находились на одной прямой. Тогда СЕ будет равна искомому расстоянию АВ.[4]

После этой справки учитель задает вопрос, а прав ли Фалес, утверждая, что СЕ=АВ. Ответы учеников могут разделиться. Далее учитель вводит теорему: «Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны». Пользуясь данной теоремой, ученики без труда ответят, что треугольники АВД и СЕД равны, а значит и соответственные стороны АВ и СЕ равны.

Проследим мотивационный этап работы над теоремой на примере теоремы: «В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой».

Один из приемов мотивации изучения данной теоремы – знание теоремы для решения задач.

В

С

Можно использовать другой прием, показав конструкцию строительной фермы (рис.3), где АС=СВ, АД=ДВ, ДМ=МВ; простейшую конструкцию стропил (рис.4) АВ=ВС и АК=КС, то есть наблюдение жизненных фактов.

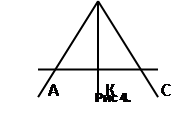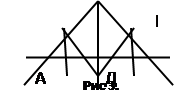Великая педагогика:

Практические упражнения для развития наблюдательности, фантазии и воображения
Для художника рисунок служит одновременно средством познания и тем предметно-образным языком, при помощи которого он общается со зрителем, воздействует на него, передает свое отношение к действительности. Органы зрения, воспринимая внешний мир, дают возможность нашему сознанию ощущать разнообразные ...

Структура педагогических способностей
В соответствии общим определением способностей, педагогические способности — это индивидуальные устойчивые свойства личности, состоящие в специфической чувствительности к объекту, средствам, условиям педагогического труда и созданию продуктивных моделей формирования искомых качеств в личности воспи ...

Развитие произвольного поведения у детей с общим недоразвитием речи
С целью выявления особенностей развития произвольного поведения детей с нарушением речи дадим психолого-педагогическую характеристику детей с нарушением речи. Несмотря на различную природу дефектов, у детей с нарушением речи имеются типичные проявления, указывающие на системное нарушение речевой де ...